A linked list is a linear data structure that is used to store a collection of data. Unlike an array, which stores data in a contiguous block of memory, a linked list consists of a series of nodes, where each node contains a reference to the next node in the list. This allows elements to be efficiently inserted and removed at any point in the list, as the only operation required is to update the references of the surrounding nodes.
Of course, it’s recommended to know the basics of the linked list before moving forward. Read more about singly linkedlist from here.
In this article we are going to look at a pattern of problems in linked list called Fast and slow pointer or Hare and tortoise.
Here is a simple linked list implementation in java with a push method that adds a node to the end of the list.
public class LinkedList {
// Inner class to represent a node in the list
private static class Node {
private int data;
private Node next;
public Node(int data) {
this.data = data;
this.next = null;
}
}
// Field to keep track of the head of the list
private Node head;
// Constructor to initialize an empty linked list
public LinkedList() {
this.head = null;
}
// Method to add a new element to the end of the list
public void add(int data) {
// Create a new node to hold the data
Node newNode = new Node(data);
// If the list is empty, set the new node as the head of the list
if (head == null) {
head = newNode;
}
// Otherwise, find the last node in the list and set its next reference
// to the new node
else {
Node current = head;
while (current.next != null) {
current = current.next;
}
current.next = newNode;
}
}
}1. Middle of the Linked list
This is the most basic example of fast and slow pointer problem in linked list.
Given a linked list with the following nodes -

To find the middle of this list which is 30, we can approach this by following ways
1. looping over all the nodes and finding length. Then run the next loop half the length of the list.
public Node middleNode(Node head) {
Node temp = head;
int length = 0;
//loop over till our pointer become null
while(temp!=null){
temp = temp.next;
length++; //increase length by one
}
Node mid = head;
// forward mid Node up till half of length
for(int i=0;i<length/2;i++){
mid = mid.next;
}
return mid;
}But with this approach, we are traversing the list 2 times, which can be further optimized.
2. Using fast and slow pointer
Let’s imagine a problem, there are 2 trains, one is faster running with 2x speed and the other is slower with x speed. They have to cover 100km distance.
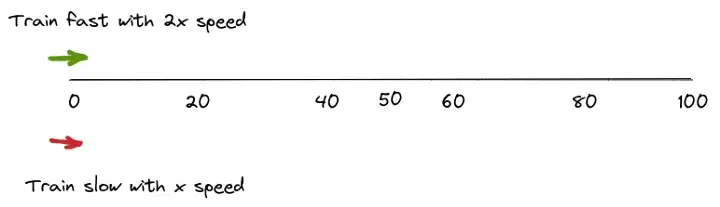
For sure, faster train is going to reach its destination earlier, when fast covers 100km, slower is going to cover half of its destination at that time, as it is moving at half the speed of faster train.

Now using this technique, we can keep two pointers at the head of our list, fast and slow pointer. we will start moving them, fast by 2 step and slow by 1 step. Then at point where fast will be at the end, slow pointer is going to be our mid pointer.
public Node middleNode(Node head) {
Node fast = head;
Node slow = head;
// Here is one tricky part, while giving condition of loop
// For list with even length, fast pointer is going to reach end i.e. null
// For off length, fast pointer is going to be at the tail
// so we have to terminate the loop
// if fast becomes null && fast.next becomes null
while( fast!=null && fast.next!=null){
// moving fast by 2 step
fast = fast.next.next;
slow = slow.next;
}
return slow;
}
solve the above problem on leetcode
2. Nth node from the end of the Linked list
Another classic problem based on fast and slow pointer. Here given a list of nodes. Return the nth node from the end.
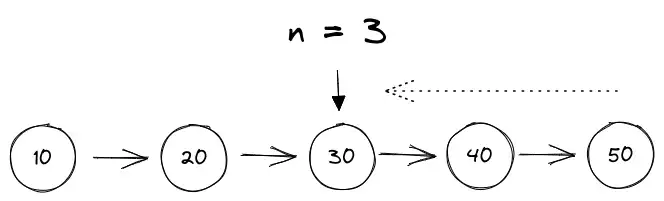
To solve this problem with fast and slow method. Our intuition should be creating a gap of n between our fast and slow pointer. So that when both are moved by one and fast becomes null, the slow pointer will be n step before the fast pointer which is null.
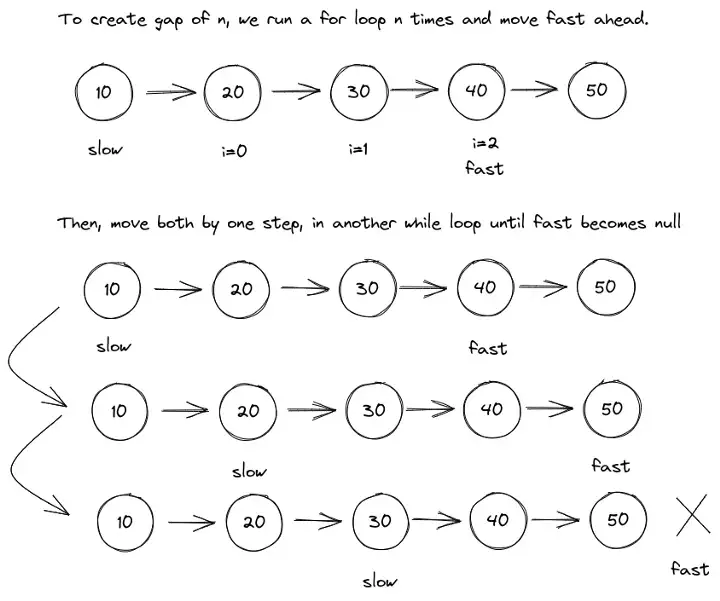
public getNodeFromEnd(Node head, int n){
Node fast = head;
Node slow = head;
//moving fast ahead by n, to make gap
for(int i=0;i<n;i++){
fast = fast.next;
}
// when the fast reaches end, slow will be the nth node from end
while(fast.next!=null){
fast = fast.next;
slow = slow.next;
}
return slow;
}
// NOTE: in case n is more than length of list, handle that case according to
// problem givenNow there is a problem related to it on leetcode.
3. Remove nth node from the end of the Linked list
We have seen how we can get the nth node from the end of the list. Now we just have to remove it. The Only difference from the previous problem is we just have to be careful of the edge cases of removing the proper node according to the question. Examples are given below -
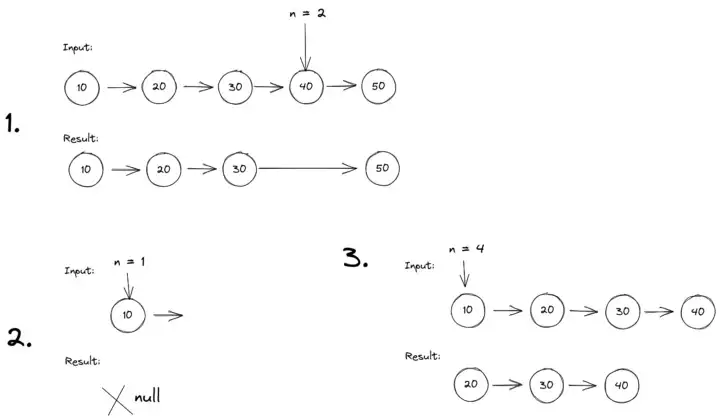
Now to solve the second case, we just need a check if head.next==null , in this case, there is only 1 element and we need to remove it, and return null.
To solve the first case, we need to follow the same method as the previous question of creating a gap of n, and then moving slow and fast by one until fast becomes null. The only difference here is, to break the link of the nth node from the end, we want to move to just the previous node of the nth node to break the chain by doing slow.next=slow.next.next; . To achieve this, we will move fast pointer just before it becomes null, so that slow will point previous of the nth node from the end, i.e. while(fast.next!=null){} .
Now for case 3rd, when n = length of list, we need to remove the head of the list. So if we followed the previous algorithm, we would reach null while moving fast pointer n times ahead. Now to solve it, we will add a check after moving fast ahead by n that, if fast==null return head.next. Because in this case, we want to delete the head.
public Node removeNthFromEnd(Node head, int n) {
Node fast = head;
Node slow = head;
// if there is only one node in list, then we can only delete that
if(head.next==null) return null;
//move fast ptr forward by n
for(int i=0;i<n;i++){
fast = fast.next;
}
// if fast becomes null, means we want to delete head
if(fast == null) return head.next;
while(fast.next!=null){
fast = fast.next;
slow = slow.next;
}
// break link from next
slow.next = slow.next.next;
// return head
return head;
}Solve this problem on leetcode.
4. Detect loop in the Linked list
At this point, this is going to be a cheesecake problem. Given a list determine whether there is a cycle or loop in the list. There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer.
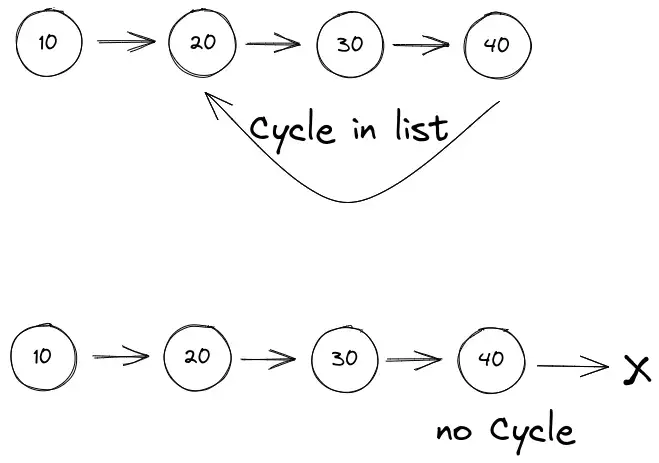
Just feel the flow of the algorithm, if there is a fast pointer moving 2 steps a time and a slow pointer moving 1 step. There is going to be a point where both fast and slow are going to collide.
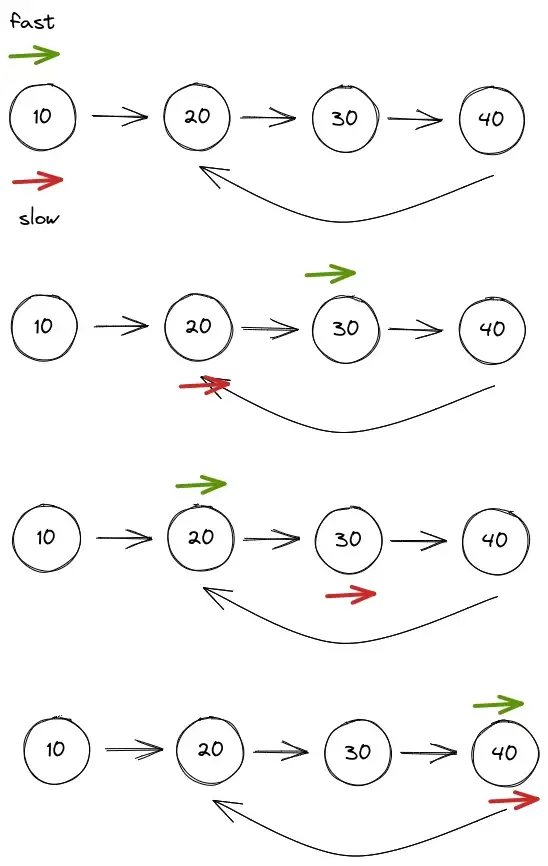
Thus to solve this. we just need a check if slow == fast at any point.
public boolean hasCycle(Node head) {
Node slow = head;
Node fast = head;
// if there is cycle, fast is never going to be null
// if there is no cycle, fast or fast.next whichever becomes null,return false
while(fast!=null && fast.next!=null){
slow = slow.next;
fast = fast.next.next;
if(slow==fast)return true;
}
return false;
}Solve this problem on leetcode
5. Find the starting point of loop in the Linked list
Given the problem, if there is a loop in the list, find the starting point where loop has started. In the following example, the loop has started from node 20. We have to return the node.
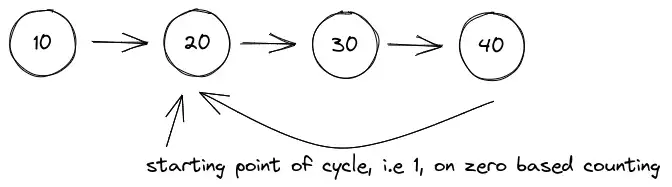
One brute-force way of doing this problem would be, maintaining a hashmap of nodes visited. If you visit the node again, which you will, in case of a loop. That node is going to be our first node of the loop.
As the above method will take O(N) space complexity of using a map, so to further optimize this code, we can use fast and slow pointer methods.
The approach will be almost the same as the previous one, we have to move fast by two-step and slow by 1. when fast and slow meet, It’s not necessary that they will meet at the start of the cycle.
So to find the starting point. When they meet, point start to head again, and move fast by 1 step and slow by 1 step. And finally they will meet at the starting point of cycle.
Let’s see how it works.
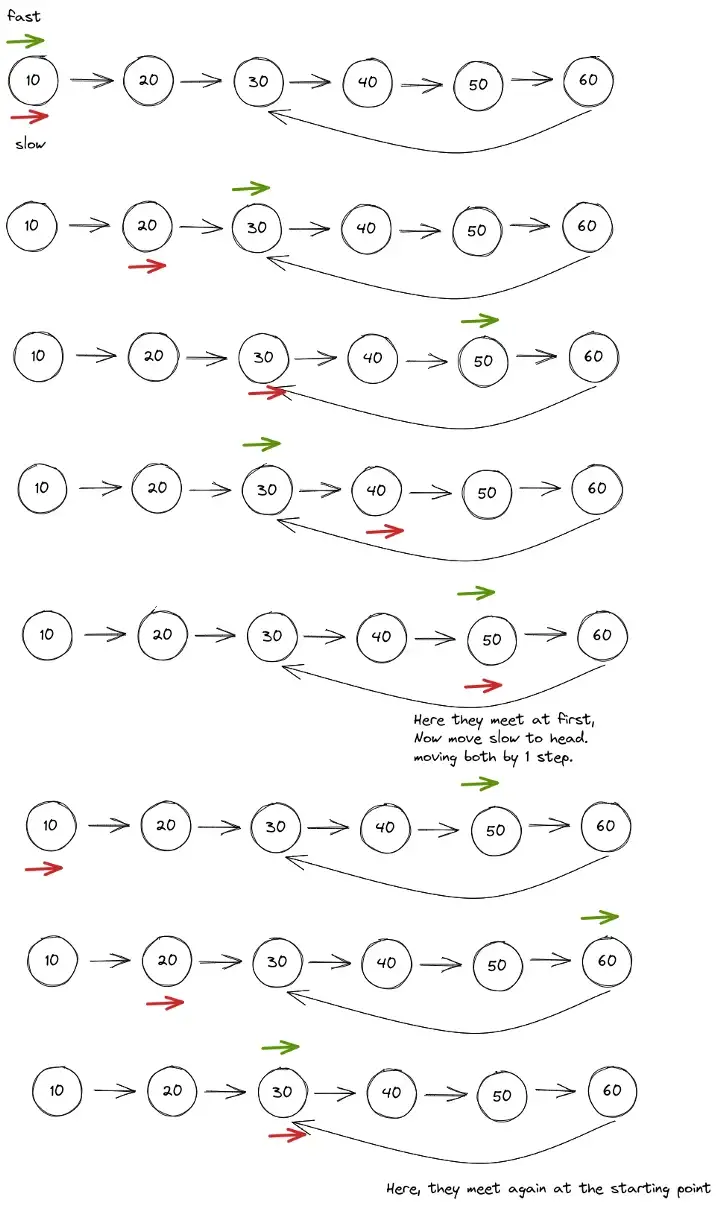
public Node detectCycle(Node head) {
Node slow = head;
Node fast = head;
while(fast!=null && fast.next!=null){
slow = slow.next;
fast = fast.next.next;
if(slow==fast){
slow = head; //moved slow to head
// moving fast and slow pointer by 1 step until they meet again
while(fast!=slow){
slow = slow.next;
fast = fast.next;
}
return slow;
}
}
return null;
}It’s a bit mathematical to explain why they both meet when slow start from head and the fast pointer from the meeting point by 1 step. To deeply understand this, I recommend going through this leetcode discuss thread.
6. Remove Loop in the Linked List
To remove the loop in the cycle we need to know when we are the last node of the list. The whole approach is just going to be the same as the previous question, but in this case, we want the tail node.
So the solution is, When fast and slow pointers meet for the first time, we point slow to the head and start another loop moving both pointer 1 step at a time. In the previous question, we break the inner loop when they meet again. But to find the last node, we need to understand that, when slow will be at the position before starting node of cycle and fast will also be at the previous node of entry point of cycle, which is the last node. Both will point the same node.
Let’s see with an example -
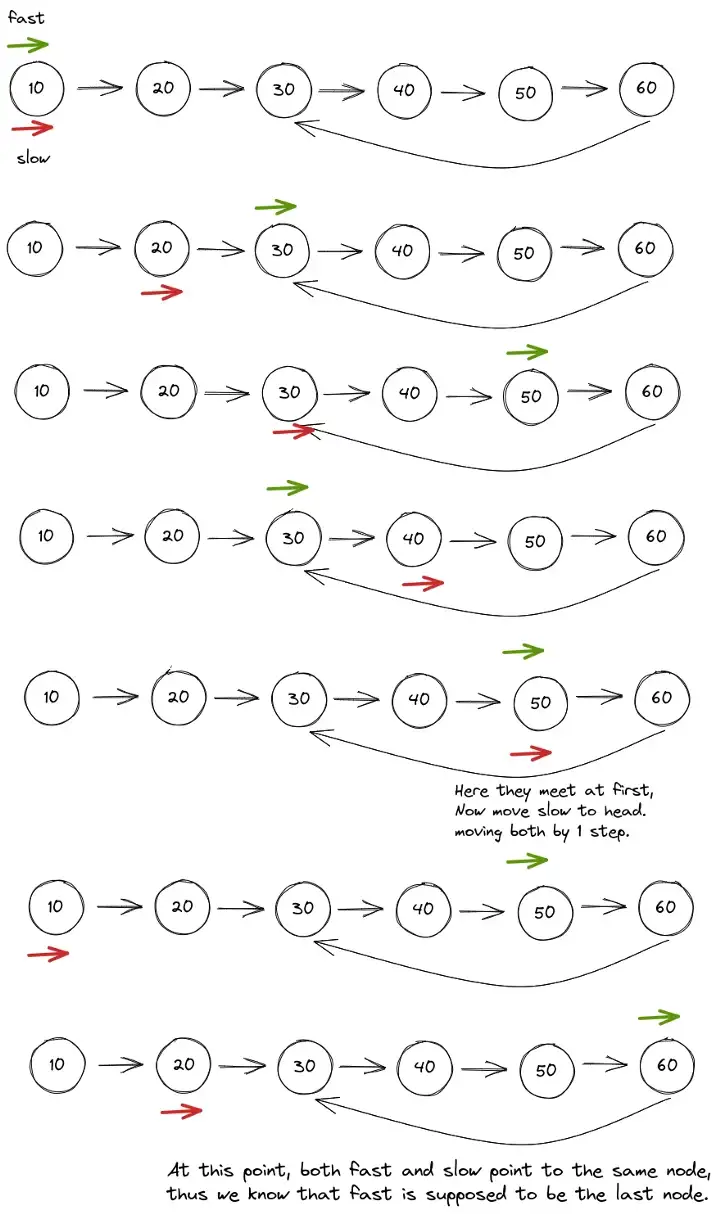
public void removeCycle(Node head) {
Node slow = head;
Node fast = head;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
if (slow == fast) {
slow = head;
//when both slow and fast point to the same node break the loop
while (slow.next != fast.next) {
slow = slow.next;
fast = fast.next;
}
// point fast to null, to remove the cycle
fast.next = null;
}
}
}solve this problem on geeksforgeeks
That’s the wrap-up for problems on the pattern of Fast and Slow pointers in the linked list. Hope you got the idea of how we use this pattern to solve problems.
Thanks!